The Triangle
The first two dimensional shape we encounter is the triangle. Three points, three lines, three angles. Length and width (base and height). Three is our first step out of abstraction, and into the visible, the intelligible, that which has form.

The triangle can contain space, dividing it into 'inside' and 'outside' the triangle. Granted, it's only 2 dimensions, but there are clear demarcations.
I think this is why the Christian God is a Trinity. Creation is finite. It is contained, and it is contained within God: Father, Son, and Holy Spirit. Within, Creation. Without... ??? Void? Nameless, immeasurable, incomprehensible nothing? Maybe it's Trinity all the way out...
The Triangle shows up everywhere.
It forms the basis of all the alchemical elemental symbols. They come to us from Agrippa,* and now seem fairly universally used in Western Alchemy.
Three is the number of Binah, the first Sephira on the Tree that relates to form, existence. The first that has a planetary attribution (Saturn). In Modern Kabbalistic thought, the tree is divided into three triangles: Supernal, Ethical, and Astral (Malkuth hangs out below, by itself. Odd circle out of triangular groupings. )
This is also an illustration of the increasing multiplicity of form. 1->2->3, all prime, all only sub-dividable by themselves, and 1 (in a whole number environment).
Greek philosophers love triangles. Pythagoras, Plato, Proculus, all had thoughts about them. Pythagoras' theorem about right triangles is famous to this day ( a2 + b2 = c2). His theory about triples is commented on by Proculus:
With points, and lines, the avenues of exploration are limited. Points are most limited, lines less so but still, there's only one dimension. With the advent of the triangle, the third, the avenues become so much greater as to be nearly limitless. This is analogous to the Daoist cosmoligical idea of the 1, the 2, and the 10,000 things.

The triangle can contain space, dividing it into 'inside' and 'outside' the triangle. Granted, it's only 2 dimensions, but there are clear demarcations.
I think this is why the Christian God is a Trinity. Creation is finite. It is contained, and it is contained within God: Father, Son, and Holy Spirit. Within, Creation. Without... ??? Void? Nameless, immeasurable, incomprehensible nothing? Maybe it's Trinity all the way out...
The Triangle shows up everywhere.
It forms the basis of all the alchemical elemental symbols. They come to us from Agrippa,* and now seem fairly universally used in Western Alchemy.
Three is the number of Binah, the first Sephira on the Tree that relates to form, existence. The first that has a planetary attribution (Saturn). In Modern Kabbalistic thought, the tree is divided into three triangles: Supernal, Ethical, and Astral (Malkuth hangs out below, by itself. Odd circle out of triangular groupings. )
This is also an illustration of the increasing multiplicity of form. 1->2->3, all prime, all only sub-dividable by themselves, and 1 (in a whole number environment).
Greek philosophers love triangles. Pythagoras, Plato, Proculus, all had thoughts about them. Pythagoras' theorem about right triangles is famous to this day ( a2 + b2 = c2). His theory about triples is commented on by Proculus:
Certain methods for the discovery of triangles of this kind are handed down, one which they refer to Plato, and another to Pythagoras. (The latter) starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it takes the square of it, subtracts unity and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side, the hypotenuse.
...For the method of Plato argues from even numbers. It takes the given even number and makes it one of the sides about the right angle; then, bisecting this number and squaring the half, it adds unity to the square to form the hypotenuse, and subtracts unity from the square to form the other side about the right angle. ... Thus it has formed the same triangle that which was obtained by the other method.Or, as Wikipedia explains the formulas:
a is odd (Pythagoras, c. 540 BC):
a is even (Plato, c. 380 BC):
With points, and lines, the avenues of exploration are limited. Points are most limited, lines less so but still, there's only one dimension. With the advent of the triangle, the third, the avenues become so much greater as to be nearly limitless. This is analogous to the Daoist cosmoligical idea of the 1, the 2, and the 10,000 things.

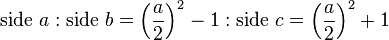

Comments